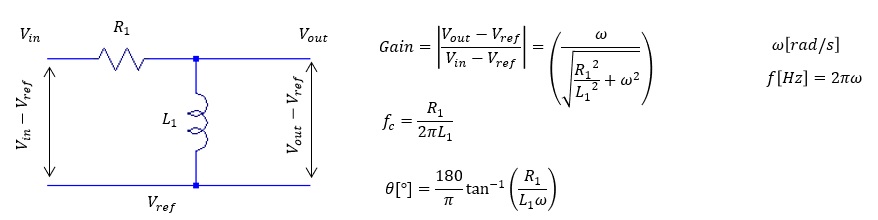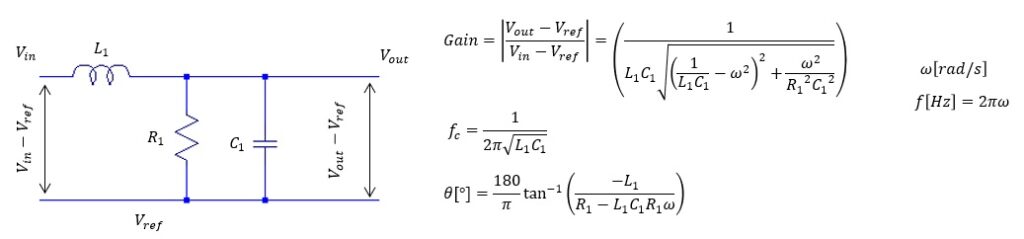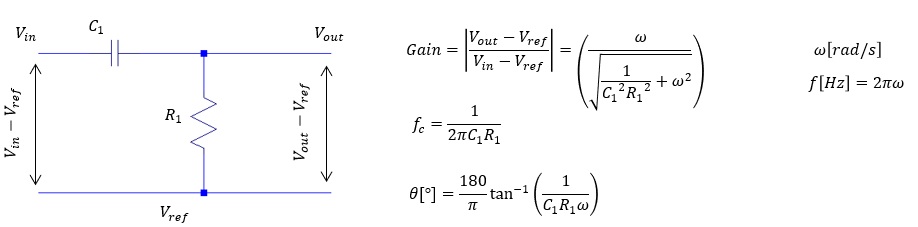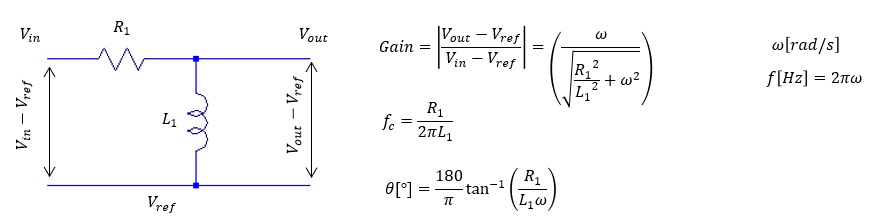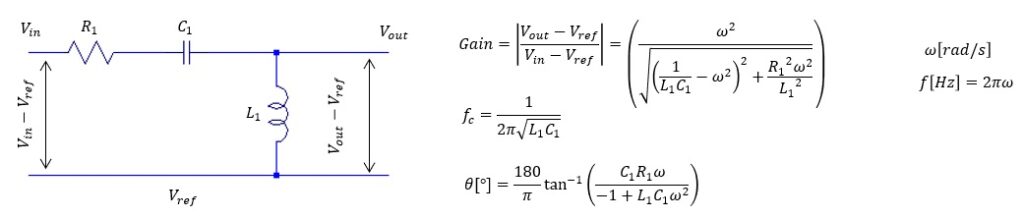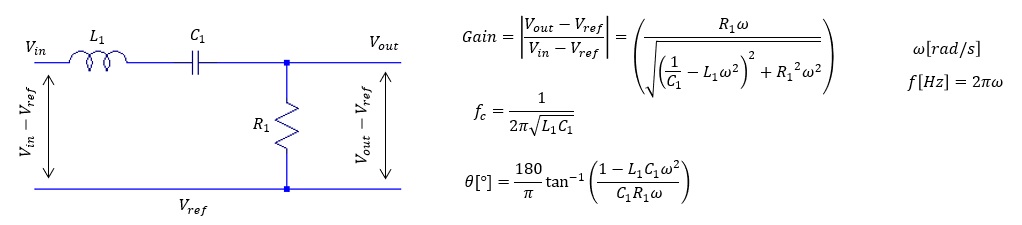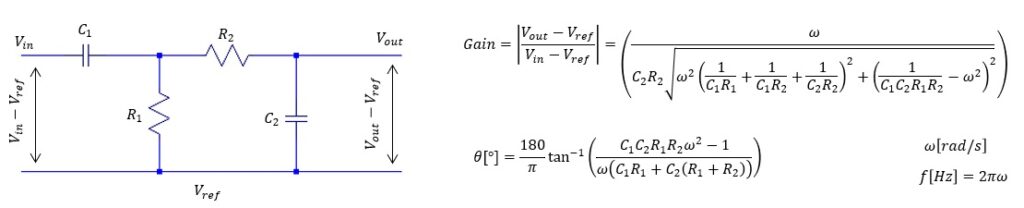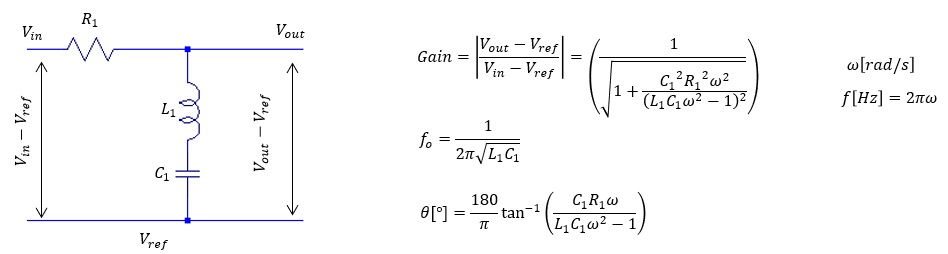このページでわかること。
- 回路の動作原理
- 応用回路の数式の見方と意味
- 応用回路をエクセルで計算する方法
電子回路の基本
ここだけは理解しておかないと以降の話はさっぱりになるので述べておきます。
回路の基本1 オームの法則
電圧V=抵抗R×電流I
回路の基本2 キルヒホッフの法則
I=I1+I2
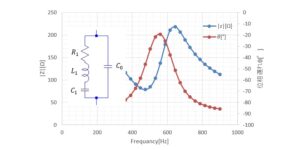
回路の基本3 インピーダンス
周波数が絡んでくると抵抗のことをインピーダンスに置き変えて計算します。
抵抗、コンデンサ、コイルをインピーダンスであらわすと、抵抗はZR、コンデンサZC、コイルZLとすると以下の様に置き変えられます。ωは角周波数[rad/sec]、jは虚数。これはこういうもんだと覚えておいてもらえればと思います。
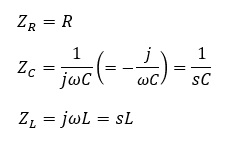
ただ、虚数があると実際にはどうしたら?と思う人も多いと思いますので、このサイトでは計算結果から虚数が無いようにしています。
周波数とノイズの抑制
アナログセンサーを使おうとすると必ず必要になる増幅とノイズカット。センサーの出力自体は小さいので100倍や1000倍と増幅して使用します。その時、ノイズも同じように増幅されてしまいます。ノイズというのは大抵センサー出力と違う周波数なのでセンサーの出力のみを取り出せるようにフィルター回路も使用します。
周波数と増幅率Gainと位相遅れθ
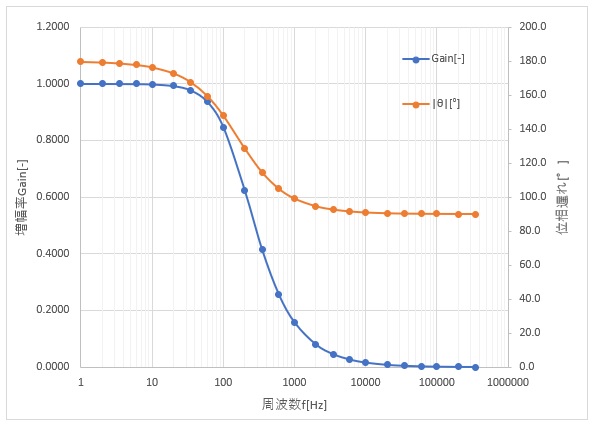
増幅率は振幅がどれだけされるかとなります。あくまで振幅です。入力×増幅率=出力となります。普通はdBで表示されますが、dBだと分かりにくいのでこのサイトではdB表記していません。dBにするときは、20LN(出力/入力)としてください。
位相遅れは、Sin波の周波数のずれと思っておいていただければと思います。
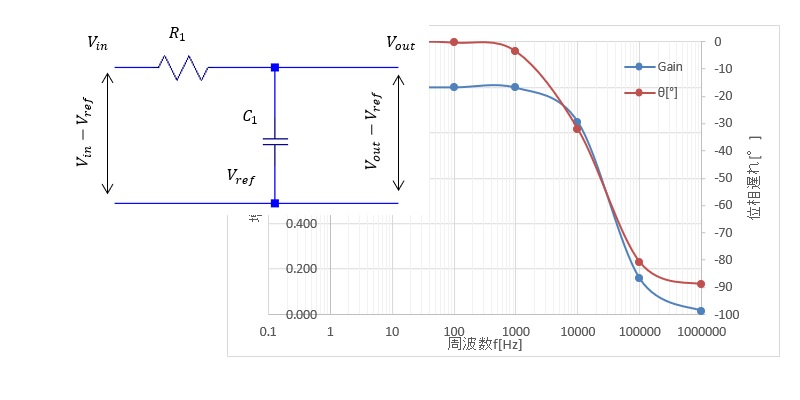
例えば、上の図で10000Hzのときを実際にオシロスコープなどで測定すると、振幅はほぼゼロと位相がほぼ90°ずれています入力のSin波に対して出力のSin波が小さく、90°ずれて観測されます。
代表的なパッシブフィルター回路の増幅率Gainと位相遅れθ
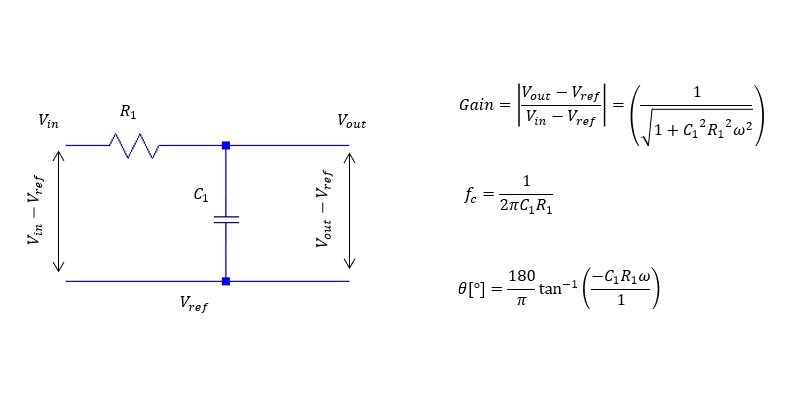
- RC ローパスフィルター
-

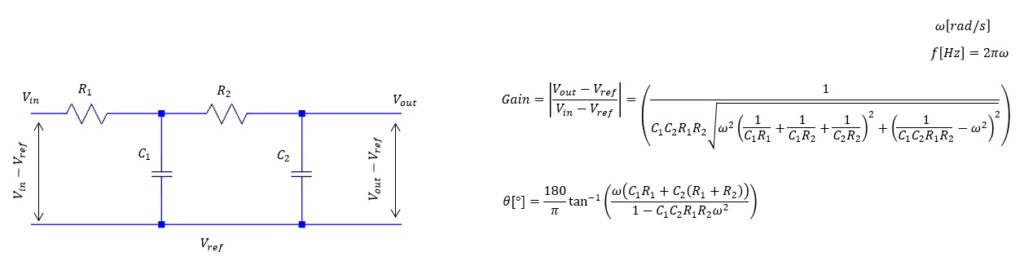
- RC 2次ローパスフィルタ
-

- LR ローパスフィルター
-

- LRC ローパスフィルター
-

- RC ハイパスフィルター
-

- RC 2次ハイパスフィルター
-

- LR ハイパスフィルター
-

- RLC ハイパスフィルター
-

- RLC バンドパスフィルター
-

- CRRC バンドパスフィルター
-

- RLC バンドエリミネーションフィルター
-

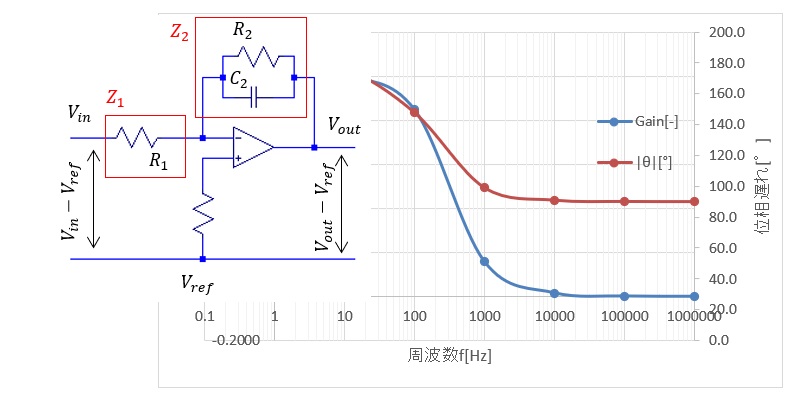
オペアンプを使ったアクティブフィルター
オペアンプの計算のポイント
オペアンプのフィルター計算のポイント
- +とーの入力端子の電圧は同じ ※(出力端子とーの入力端子が電気的につながってるとき)
- 入力端子には電流は流れない
オペアンプはなんか良くわからないという人が多いと思います。じつは、計算をするとき2つのポイントだけ理解していれば簡単に扱えます。
代表的なオペアンプの使い方を紹介